rsync 的核心算法
rsync是unix/linux下同步文件的一个高效算法,它能同步更新两处计算机的文件与目录,并适当利用查找文件中的不同块以减少数据传输。rsync中一项与其他大部分类似程序或协定中所未见的重要特性是镜像是只对有变更的部分进行传送。rsync可拷贝/显示目录属性,以及拷贝文件,并可选择性的压缩以及递归拷贝。rsync利用由Andrew Tridgell发明的算法。这里不介绍其使用方法,只介绍其核心算法。我们可以看到,Unix下的东西,一个命令,一个工具都有很多很精妙的东西,怎么学也学不完,这就是Unix的文化啊。
本来不想写这篇文章的,因为原先发现有很多中文blog都说了这个算法,但是看了一下,发现这些中文blog要么翻译国外文章翻译地非常烂,要么就是介绍这个算法介绍得很乱让人看不懂,还有错误,误人不浅,所以让我觉得有必要写篇rsync算法介绍的文章。(当然,我成文比较仓促,可能会有一些错误,请指正)
目录
问题
首先, 我们先来想一下rsync要解决的问题,如果我们要同步的文件只想传不同的部分,我们就需要对两边的文件做diff,但是这两个问题在两台不同的机器上,无法做diff。如果我们做diff,就要把一个文件传到另一台机器上做diff,但这样一来,我们就传了整个文件,这与我们只想传输不同部的初衷相背。
于是我们就要想一个办法,让这两边的文件见不到面,但还能知道它们间有什么不同。这就出现了rsync的算法。
算法
rsync的算法如下:(假设我们同步源文件名为fileSrc,同步目的文件叫fileDst)
1)分块Checksum算法。首先,我们会把fileDst的文件平均切分成若干个小块,比如每块512个字节(最后一块会小于这个数),然后对每块计算两个checksum,
- 一个叫rolling checksum,是弱checksum,32位的checksum,其使用的是Mark Adler发明的adler-32算法,
- 另一个是强checksum,128位的,以前用md4,现在用md5 hash算法。
为什么要这样?因为若干年前的硬件上跑md4的算法太慢了,所以,我们需要一个快算法来鉴别文件块的不同,但是弱的adler32算法碰撞概率太高了,所以我们还要引入强的checksum算法以保证两文件块是相同的。也就是说,弱的checksum是用来区别不同,而强的是用来确认相同。(checksum的具体公式可以参看这篇文章)
2)传输算法。同步目标端会把fileDst的一个checksum列表传给同步源,这个列表里包括了三个东西,rolling checksum(32bits),md5 checksume(128bits),文件块编号。
我估计你猜到了同步源机器拿到了这个列表后,会对fileSrc做同样的checksum,然后和fileDst的checksum做对比,这样就知道哪些文件块改变了。
但是,聪明的你一定会有以下两个疑问:
- 如果我fileSrc这边在文件中间加了一个字符,这样后面的文件块都会位移一个字符,这样就完全和fileDst这边的不一样了,但理论上来说,我应该只需要传一个字符就好了。这个怎么解决?
- 如果这个checksum列表特别长,而我的两边的相同的文件块可能并不是一样的顺序,那就需要查找,线性的查找起来应该特别慢吧。这个怎么解决?
很好,让我们来看一下同步源端的算法。
3)checksum查找算法。同步源端拿到fileDst的checksum数组后,会把这个数据存到一个hash table中,用rolling checksum做hash,以便获得O(1)时间复杂度的查找性能。这个hash table是16bits的,所以,hash table的尺寸是2的16次方,对rolling checksum的hash会被散列到0 到 2^16 – 1中的某个整数值。(对于hash table,如果你不清楚,建议回去看大学时的数据结构教科书)
顺便说一下,我在网上看到很多文章说,“要对rolling checksum做排序”(比如这篇和这篇),这两篇文章都引用并翻译了原作者的这篇文章,但是他们都理解错了,不是排序,就只是把fileDst的checksum数据,按rolling checksum做存到2^16的hash table中,当然会发生碰撞,把碰撞的做成一个链表就好了。这就是原文中所说的第二步——搜索有碰撞的情况。
4)比对算法。这是最关键的算法,细节如下:
4.1)取fileSrc的第一个文件块(我们假设的是512个长度),也就是从fileSrc的第1个字节到第512个字节,取出来后做rolling checksum计算。计算好的值到hash表中查。
4.2)如果查到了,说明发现在fileDst中有潜在相同的文件块,于是就再比较md5的checksum,因为rolling checksume太弱了,可能发生碰撞。于是还要算md5的128bits的checksum,这样一来,我们就有 2^-(32+128) = 2^-160的概率发生碰撞,这太小了可以忽略。如果rolling checksum和md5 checksum都相同,这说明在fileDst中有相同的块,我们需要记下这一块在fileDst下的文件编号。
4.3)如果fileSrc的rolling checksum 没有在hash table中找到,那就不用算md5 checksum了。表示这一块中有不同的信息。总之,只要rolling checksum 或 md5 checksum 其中有一个在fileDst的checksum hash表中找不到匹配项,那么就会触发算法对fileSrc的rolling动作。于是,算法会住后step 1个字节,取fileSrc中字节2-513的文件块要做checksum,go to (4.1) – 现在你明白什么叫rolling checksum了吧。
4.4)这样,我们就可以找出fileSrc相邻两次匹配中的那些文本字符,这些就是我们要往同步目标端传的文件内容了。
rolling checksum算法
这个算法很简单,也叫Rabin-Karp 算法,由 Richard M. Karp 和 Michael O. Rabin 在 1987 年发表,它也是用来解决多模式串匹配问题的。其最大的精髓是,当我们往后面step 1个字符的时候,不用全部重新计算所有的checksum,也就是说,我们从 [0, 512] rolling 到 [1, 513] 时,我们不需要重新计算从1到513的checksum,而是重用 [0,512]的checksum直接算出来。
这个算法比较简单,我举个例子,我们有一个数字:12345678,假设我们以5个长度作为一个块,那么,第一个块就是 12345 ,12345可以表示为:
1 * 10^4 + 2 * 10^3 + 3 * 10^2 + 4 * 10^1 + 5 * 10^0 = 12345
如果我们要step 1步,也就是要得到 23456, 我们不必计算:
2 * 10^4 + 3 * 10^3 + 4 * 10^2 + 5 * 10^1 + 6 * 10^0
而是直接计算:
(12345 - 1 * 10^4) * 10 + 6 * 10 ^0
我们可以看到,其中,我们把12345最左边第一位去掉,然后,再加上最右边的一位。这就是Rolling checksum的算法。
实际的公式是:
hash ( t[0, m-1] ) = t[0] * b^(m-1) + t[1] * b^[m-2] ..... t[m-1] * b^0
其中的 b是一个常数基数,在 Rabin-Karp 算法中,我们一般取值为 256。
于是,在计算 hash ( t[1, m] ) 时,只需要下面这样就可以了:
hash( t[1, m] ) = hash ( t[0, m-1] ) - t[0] * b^(m-1) + t[m] * b ^0
图示
怎么,你没看懂? 好吧,我送佛送上西,画个示意图给你看看(对图中的东西我就不再解释了)。
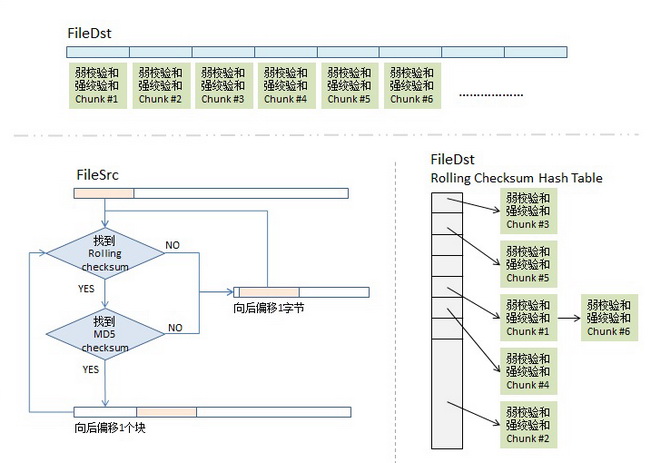
这样,最终,在同步源这端,我们的rsync算法可能会得到下面这个样子的一个数据数组,图中,红色块表示在目标端已匹配上,不用传输(注:我专门在其中显示了两块chunk #5,相信你会懂的),而白色的地方就是需要传输的内容(注意:这些白色的块是不定长的),这样,同步源这端把这个数组(白色的就是实际内容,红色的就放一个标号)压缩传到目的端,在目的端的rsync会根据这个表重新生成文件,这样,同步完成。

最后想说一下,对于某些压缩文件使用rsync传输可能会传得更多,因为被压缩后的文件可能会非常的不同。对此,对于gzip和bzip2这样的命令,记得开启 “rsyncalbe” 模式。
(全文完,转载时请注明作者和出处)
(转载本站文章请注明作者和出处 宝酷 – sou-ip ,请勿用于任何商业用途)




 (41 人打了分,平均分: 4.46 )
(41 人打了分,平均分: 4.46 )
《rsync 的核心算法》的相关评论
刚好非常需要这篇文章!先谢谢了!
There’s no rsyncable switch in bzip2. bzip2 is a block based compression algorithm, no hash based block split mechanism is used.
wikipedia上说的很清楚 —— “Some compression programs, such as gzip and bzip2, provide a special “rsyncable” mode which allows these files to be efficiently rsynced”
算法讲的很清楚,赞~~
怒赞!
“rsync利用由澳洲电脑程式师” –> 说法好台湾啊~
哈哈,我是从wikipedia上copy+paste过来的。见笑了。
在某些极端例子中,源及目的文件完全不同,rsync将会导致逐一step 1 bytes进行比较,然后在完整sync整个文件。我感觉这种情况下,rsync性能就很差了? rsync的设计初衷只是尽量减少同步信息的传输大小?
第一次没看懂,耐心看了第二次、第三次,自我感觉算是明白了。我的疑问是,diff 又是怎么一个算法呢?想一想… …
没有用过unix/linux,你很难明白diff是什么,从今天学会用unix/linux吧。
很简练,学些了,最后一行单词敲错“rsyncalbe”-> rsyncable
有一个问题。假设按512字节分块,然后在源文件中,我每隔511字节就插入一个字节,也就是我故意让每个块中的校验都不匹配,这样不就造成了整个文件传输了吗?而最优的做法是只传 文件大小/块大小(512) 个字节的数据
你很可爱哦。@Celebi
@brookechen
一般机子上, 弱 checksum 非常快, 瓶颈在磁盘上, 所以没有问题.
讲很清晰,多谢,收下了。
@Celebi
情况很少见 这是刻意的攻击了。。。
做了一下搜索,Andrew Tridgell关于排序和同步算法的博士论文:
http://www.samba.org/~tridge/phd_thesis.pdf
rsync算法的详细介绍:
http://rsync.samba.org/tech_report/
我的文章里有Andrew Tridgell的源文链接。
赞
之前也看过一些文章~ 现在才知道块不匹配时,会偏移一个字节再尝试匹配
我突然想到 不知道像dropbox这样的东西,会不会也是用类似这样的技术呢?
Samba也是这个Andrew Trigell实现的…
那个概率计算不对吧?因为散列算法不完美(近些年有所公开报导),所以真实的碰撞概率要大很多
Wikipedia : “With 128 bits from MD5 plus 32 bits from the rolling checksum, and assuming maximum entropy in these bits, the probability of a hash collision with this combined checksum is 2^−(128+32) = 2^−160.”
在实际运用时,每一块取多少个字节,才能使得对比更快并且传输数据量更少呢?(比如512字节会不会太大了,虽然对比速度快,但容易造成太多的不一致导致传输量太大了)不知道有这方面的研究没。
@宝酷
维基百科上,点击转成简体中文后应该不会显示为“程式师”呀。
陈博主,在比对算法一节中有一句:住后step一个字节。。。 住应该是往吧。不过五笔输入法不会犯这种错误,不知是哪种输入法。。。
往前,还是往后,这是我的问题,我总是分不清。从小学就分不清。sorry.
这篇文章还是意犹未尽,rolling hash这么关键的东西却没有讲清楚….
推荐大家都看看rolling hash.
http://rsync.samba.org/tech_report/node3.html
但是这两个问题在两台不同的机器上
^文件
rolling checksum 4个字节
md5 16个字节
文件块编号 4个自己
总共4+16+4=24,代表512个字节,512/24=21.333。即一个213M的文件,传checksum就要传10M,如果文件2133M,那么要传100M。假设每分钟同步一次,同步量貌似也挺大的。
不只是传输整个文件的问题,按照算法的描述,应该对整个文件进行了每个字节扫描。如果文件FileSrc 文件大小为N,那就要至少匹配(N-512)*512次··· ··· @Celebi
@吕子熏
so 我也觉得这个512的取值很有讲究
good
任何算法都是有漏洞的,你非要这样整,就忘记了用rsync的初衷。@Celebi
@ithaca
DropBox就是想把Rsync,SVN之类的整合在一块. 我们公司也用到类似的技术,但是和Rsync比较起来,感觉我们的东西太浪费资源了..
@技术宅的每日三省
对CHECKSUM再做ROLLING CHECKSUM…
@beyond_st
取512字节大小作为运算单位,估计是考虑到文件对齐的原因。磁盘扇区原先都是512字节大小。现在倒是有扇区4K大小的磁盘了.总之大小对齐是必须的.
那rsync和merkle tree比有什么优劣呢?
是的,512只是一个例子,并不是算法就设置成这样的。这个是可以通过参数输入的。另,rsync的网络传输有-z参数,压缩后再传。
@放羊娃
之前说错了..既然是ROLLING,就不需要对齐了…SORRY..
@宝酷
他说的是,往和住的区别
已转发,谢谢分享。
前几天@宝酷 叔叔在微博上常常讲rsync.有人问”rsync 能具体说说么?”答曰”自己Google去”.
默默去google,但似乎收获不大.
现在看本文,感觉好理解很多.果然宝酷出品,必属精品么
转载到 http://www.codeislife.tk/index.php/archives/175这个位置
别这样吧,没有sou-ip,就不知道怎么学啦?呵呵。
这个算法对于增量内容解释的很详细,可是如果源文件有删减内容,这个算法过程就没解释了。比如源文件第一个字节被移除,这时比对过程是怎样进行的?
一样的,因为偏移是一个字节一个字节的走的。
其实宏观上看来部分拷贝传递就和版本管理系统比较类似,每次向服务器提交的也只是此次更改所产生的差分信息。
差分以及压缩算法可能略有不同,版本管理系统更侧重于历史的回溯与重现。
@Celebi
文件大小增长了怎么办呢?
@宝酷 是的,我想错了。
说句实话,在国内找有关学术的东西,常常会失望:要么是互相copy,而且错误百出;要么是加为会员,收费下载。。。
这文章真的很不错,推荐看
@技术宅的每日三省
有个问题有点小小的不明白,
比如有个文件 [0x01,0x02,0x03,0x04,0x05,0x06,0x07,0x08,0x09]
新的文件删除了0x04这个字节,同步的时候
服务器是怎么操作的?
难道是把0x05及其以后的字节读出来然后拷贝到前一个字节?
添加了一个字节呢?
恩,很通俗易懂。
实际使用时怎么样呢?
@LEo
我觉得实际使用时的表现比理论计算要可靠
比较极端的情况好像会非常可怕, 一个1g 的文件, 有1g/512 个块, 突然换成完全不一样的一个块 2g/512. 基本完全不一致, 那么就会把一个 2g 的src 做上2g 次比较? 是这样吗?不断的step 1 进行比较。
以前在csdn讨论文件增量备份,偶自己琢磨出过类似算法……
不过偶那时还不知道rolling checksum,用了关键字标记头部+md5验证的方法。然后忽然看到澳大利亚一学生的论文,这才学会rolling checksum……